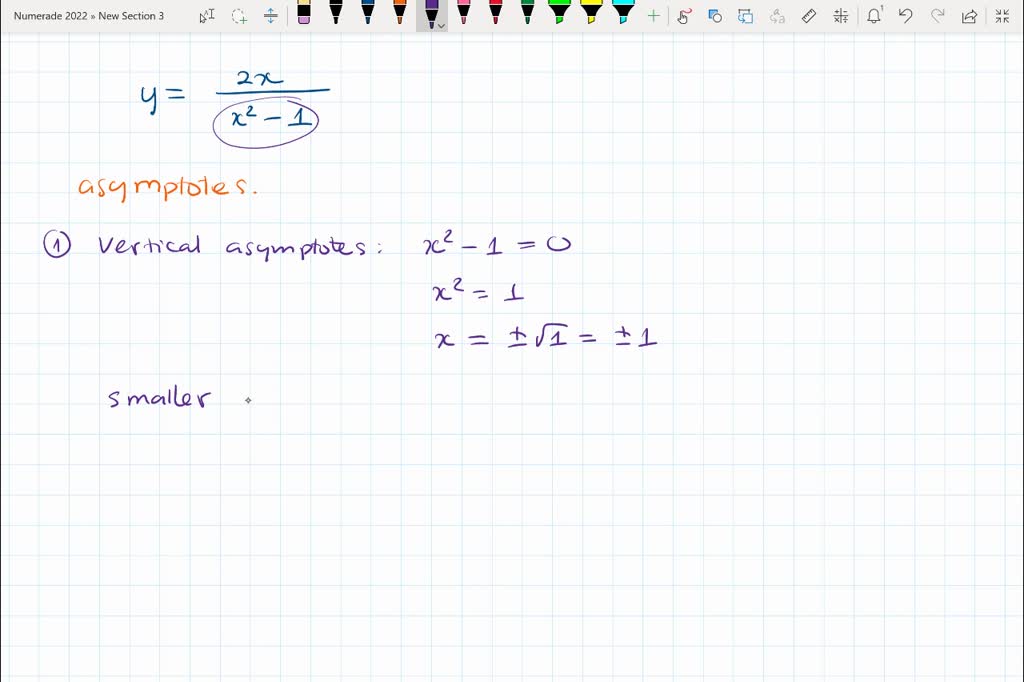Point Of Inflection Vertical Asymptote . a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. F (x) = 1 x has vertical asymptote: a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. The graph of this function is concave down on (− ∞,0) and concave up on (0,∞). Roots = solve(denom) roots =. to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. it this example, the possible point of inflection \((0,0)\) is not a point of inflection.
from www.numerade.com
it this example, the possible point of inflection \((0,0)\) is not a point of inflection. Roots = solve(denom) roots =. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. The graph of this function is concave down on (− ∞,0) and concave up on (0,∞). F (x) = 1 x has vertical asymptote:
SOLVED Analyze and sketch the graph of the function. Identify any
Point Of Inflection Vertical Asymptote vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. F (x) = 1 x has vertical asymptote: a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). Roots = solve(denom) roots =. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. The graph of this function is concave down on (− ∞,0) and concave up on (0,∞).
From www.youtube.com
Asymptotes and Curve Sketching YouTube Point Of Inflection Vertical Asymptote it this example, the possible point of inflection \((0,0)\) is not a point of inflection. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. a vertical asymptote is a place where the function becomes infinite, typically because the formula for. Point Of Inflection Vertical Asymptote.
From www.slideserve.com
PPT Logarithmic Functions PowerPoint Presentation, free download ID Point Of Inflection Vertical Asymptote vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). to find the vertical asymptotes of f, set the denominator equal. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVED Analyze and sketch the graph of the function. Identify any Point Of Inflection Vertical Asymptote a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). it this example, the possible point of inflection \((0,0)\) is not a point of inflection. a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. F (x). Point Of Inflection Vertical Asymptote.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Vertical Asymptote vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. The graph of. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVEDGive a graph of the rational function and label the coordinates Point Of Inflection Vertical Asymptote to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. The graph of this function is concave down on (− ∞,0) and concave up on (0,∞). vertical asymptotes, or va, are dashed vertical lines on a. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVED Analyze and sketch the graph of the function. Find any Point Of Inflection Vertical Asymptote Roots = solve(denom) roots =. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. a function cannot cross a vertical asymptote because the graph must approach infinity (or. Point Of Inflection Vertical Asymptote.
From sites.psu.edu
Chapter 7, Answers Math 140 Calculus and Analytic Geometry 1 Point Of Inflection Vertical Asymptote a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). Roots = solve(denom) roots =. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. vertical asymptotes, or. Point Of Inflection Vertical Asymptote.
From www.chegg.com
Solved 5. Approximate the coordinates of any inflection Point Of Inflection Vertical Asymptote Roots = solve(denom) roots =. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. it this example, the possible point of inflection \((0,0)\). Point Of Inflection Vertical Asymptote.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Vertical Asymptote vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVED Analyze and Sketch a graph of the function Identify any Point Of Inflection Vertical Asymptote a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. The. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVEDGive a graph of the rational function and label the coordinates Point Of Inflection Vertical Asymptote to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. Roots = solve(denom) roots =. a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y. Point Of Inflection Vertical Asymptote.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Vertical Asymptote to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVED point) Plot a graph of the rational function 32+8 f(x) and Point Of Inflection Vertical Asymptote vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y = f (x) denominator. Roots = solve(denom) roots =. a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. F (x) = 1. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVEDGiven the function f (x) "0! Te Jt 6l1,* acj.c 'lcv Find the Point Of Inflection Vertical Asymptote a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. F (x) = 1 x has vertical asymptote: to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of. Point Of Inflection Vertical Asymptote.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Vertical Asymptote a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). it this example, the possible point of inflection \((0,0)\) is not a point of inflection. vertical asymptotes, or va, are dashed vertical lines on a graph corresponding to the zeroes of a function y. Point Of Inflection Vertical Asymptote.
From www.numerade.com
SOLVED SCALCET9 4.3.036. Sketch the graph of a function that satisfies Point Of Inflection Vertical Asymptote a vertical asymptote is a place where the function becomes infinite, typically because the formula for the. Roots = solve(denom) roots =. to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least. Point Of Inflection Vertical Asymptote.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Vertical Asymptote to find the vertical asymptotes of f, set the denominator equal to 0 and solve it. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. a function cannot cross a vertical asymptote because the graph must approach infinity (or \( −∞\)) from at least one direction as \(x\). F (x) =. Point Of Inflection Vertical Asymptote.
From www.numerade.com
Sketch the graph of a function that satisfies all of the given Point Of Inflection Vertical Asymptote The graph of this function is concave down on (− ∞,0) and concave up on (0,∞). a function cannot cross a vertical asymptote because the graph must approach infinity (or − ∞) − ∞) from at least one direction as x x. it this example, the possible point of inflection \((0,0)\) is not a point of inflection. . Point Of Inflection Vertical Asymptote.